The Realities of Quantum Machine Learning
By Morton Swimmer
Quantum machine learning (QML) is at the nexus of two very hyped topics: artificial intelligence and quantum computing. Ignoring the AI hype, let's explore how realistic quantum machine learning is. But first we need to put one thing behind us: in the near future, we won’t have quantum computers that can scale to large enough sizes to do meaningful computations. Noise management and entangling enough qubits are just two of the problems we are still facing.
Using the small prototype machines we do have, we are getting closer to understanding their potential and limitations, but we are still in the phase of building quantum computers to understand what they will be useful for. Keep in mind that quantum computers are nothing like their classical counterparts. It is the difference between calculating with the foundations of physics versus a glorified calculator. See our previous article on quantum computing for a more detailed explanation.
We are interested in quantum machine learning because despite the hype, it is true that we need faster and more efficient computers. Moore’s law is at an end, and machine learning workloads are only getting larger. Using masses of CPUs and GPUs is becoming unsustainable in terms of energy and resource needs. On paper, quantum computers are a good fit as their forte is linear algebra, which is also at the heart of much of machine learning. These operations can be executed exponentially faster on a quantum computer — potentially. But putting quantum machine learning into practice is more complicated.
Research into QML has intensified recently and we now have quantum equivalents for many classical machine learning methods. Linear regression is one of the most fundamental algorithms (and still very useful) and it is not surprising to know that there are a variety of quantum computing approaches.
A popular approach to data clustering is the support vector machines, which also have quantum implementations (QSVM). Using these QSVMs we can implement decision tree learning, the workhorse of the industry, on a quantum computer. Non-linear regression is best handled by a quantum neural network (QNN) approach. This approach utilizes parameterized quantum circuits (PQC), or more often, variational quantum circuits (VQA). (Quantum circuits are the equivalent of runnable code on classical computers.) With the basics of QNNs available, it follows that convolutional neural networks, generative adversarial networks, and others have quantum equivalents. Hidden Markov models, useful in sequence analysis, can also be implemented.
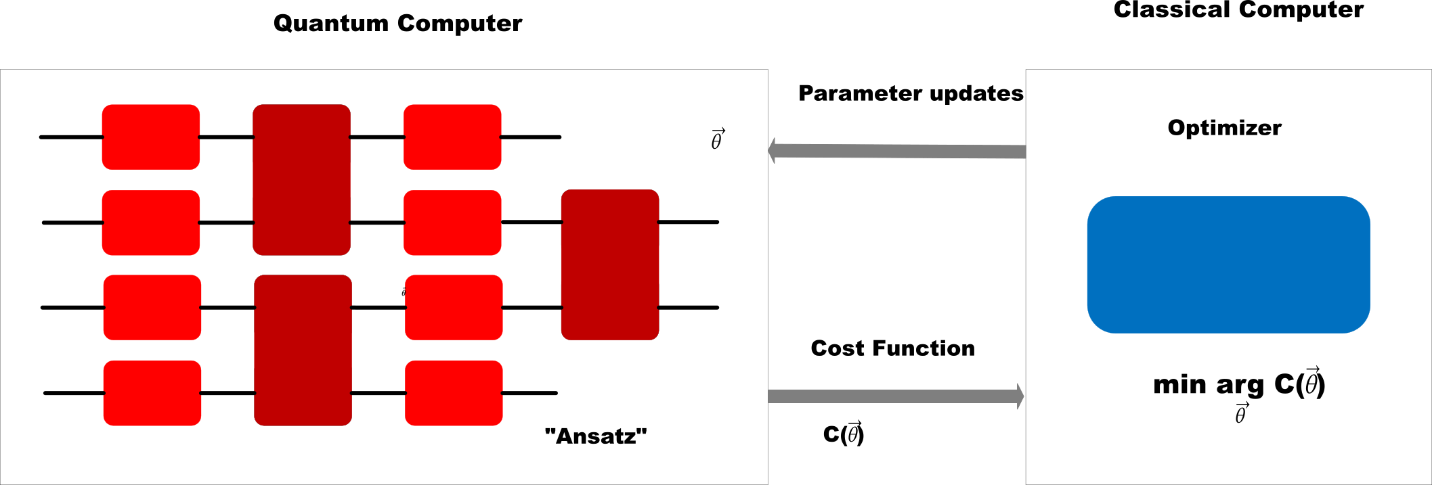
Figure 1. A representation of the VQA (Variational Quantum Algorithm) showing that there is a quantum and classical component
Many of these algorithms are already implemented in quantum computing frameworks like Qiskit, Cirq, or Pennylane. Extensions to popular machine learning libraries, like PyTorch or Tensorflow with quantum computer support, are also available. With those, we can access quantum computer simulators or even real prototype machines to test out our algorithm ideas.
Disregarding the current lack of capable quantum computers, quantum machine learning algorithms suffer from other issues as well. We can't implement back-propagation natively on a quantum computer so, as we have already mentioned, many of these algorithms rely on VQA. But the parameters these circuits use (see the vector ⦳ in Figure 1) are implemented when the circuit is loaded into the quantum computer using a template (an "Ansatz") and this needs to be done every time the parameters are updated, which happens repeatedly during the training process.
The parameters are also optimized by a classical computer which results in latency and impacts the performance of the algorithm. QNN-based machine learning also suffers from a problem called “barren plateaus.” Without some mitigation, the model becomes untrainable. Finding solutions to this problem is an active field of research and some solutions already exist. QCNNs don't exhibit this problem, though, so perhaps more novel approaches are needed to avoid such pitfalls. However, as it stands, implementing something like the attention model, the basis of GPT, is not practical.
There is not enough space to enumerate all the problems QML will have, and research may have breakthroughs that mitigate these any time, but one other fundamental problem needs mentioning. The total time it takes to load data into a quantum circuit may dwarf any speedup the quantum algorithm brings to the table. This is because the data is an intrinsic part of the circuit. In a classical function the calculation process takes in external data and spits out the results on the other side. This also means that the way things stand, we will need much better than quadratic speedup to justify a quantum implementation of algorithm, and big data applications may be out of reach until this problem is solved.
No doubt, there will be both engineering and scientific progress made to alleviate many of these problems. But for now, QML remains theoretical, rather than practical. In the future, we hope to see research done on algorithms that use the idiosyncrasies of the quantum computer properly rather than merely trying to replicate classical machine learning on a quantum computer.
This article only discussed one mode of QML: using a quantum computer to solve classical problems, although we touched upon how classical machine learning can help adjust parameters to the VQA components. Perhaps the real future of quantum machine learning will revolve around learning models from quantum data that have been generated by some other quantum process, perhaps a simulation of molecular interactions in a drug discovery experiment. For that we need larger machines that mitigate noise better and we are still waiting for those.
Like it? Add this infographic to your site:
1. Click on the box below. 2. Press Ctrl+A to select all. 3. Press Ctrl+C to copy. 4. Paste the code into your page (Ctrl+V).
Image will appear the same size as you see above.
последний
- Forecasting Future Outbreaks: A Behavioral and Predictive Approach to Proactive Cyber Risk Management
- Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report
- The Industrialization of Botnets: Automation and Scale as a New Threat Infrastructure
- From Holiday Snap to Custom Scam in 30 Minutes: How AI Turns Public Photos Into Targeted Attacks
- From LinkedIn to Tailored Attack in 30 Minutes: How AI Accelerates Target Profiling for Cybercrime

 Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report
Fault Lines in the AI Ecosystem: TrendAI™ State of AI Security Report AI Security Starts Here: The Essentials for Every Organization
AI Security Starts Here: The Essentials for Every Organization The AI-fication of Cyberthreats: Trend Micro Security Predictions for 2026
The AI-fication of Cyberthreats: Trend Micro Security Predictions for 2026 Stay Ahead of AI Threats: Secure LLM Applications With Trend Vision One
Stay Ahead of AI Threats: Secure LLM Applications With Trend Vision One