Post-Quantum Cryptography: Migrating to Quantum Resistant Cryptography
By Morton Swimmer, Mark Chimley, Adam Tuaima
In the previous parts of this series, we have learned about cryptography, what makes quantum computers unique, and how quantum computers break this cryptography. In the fourth and final part of our study on post-quantum cryptography, we will look at quantum-resistant algorithms that could replace our existing cryptography.
Algorithmic Assumptions
The algorithmic assumption of most existing public key cryptography in common use is that factoring large integers is hard; because of quantum computers and Shor’s algorithm, this algorithmic assumption is now a vulnerability. We need new assumptions that are quantum resistant, easy to solve if we know the key, but practically impossible to solve without the key on both classical and quantum computers. In the following sections, we get into commonly discussed schemes to solve these new requirements.
Learning with errors
Learning with errors (LWE) is based on the idea of representing secret information as a set of equations and then intentionally introducing errors to hide the real value of the hidden information. There are several variants of this, such as ring learning with errors (RLWE) and module learning with errors (MLWE).
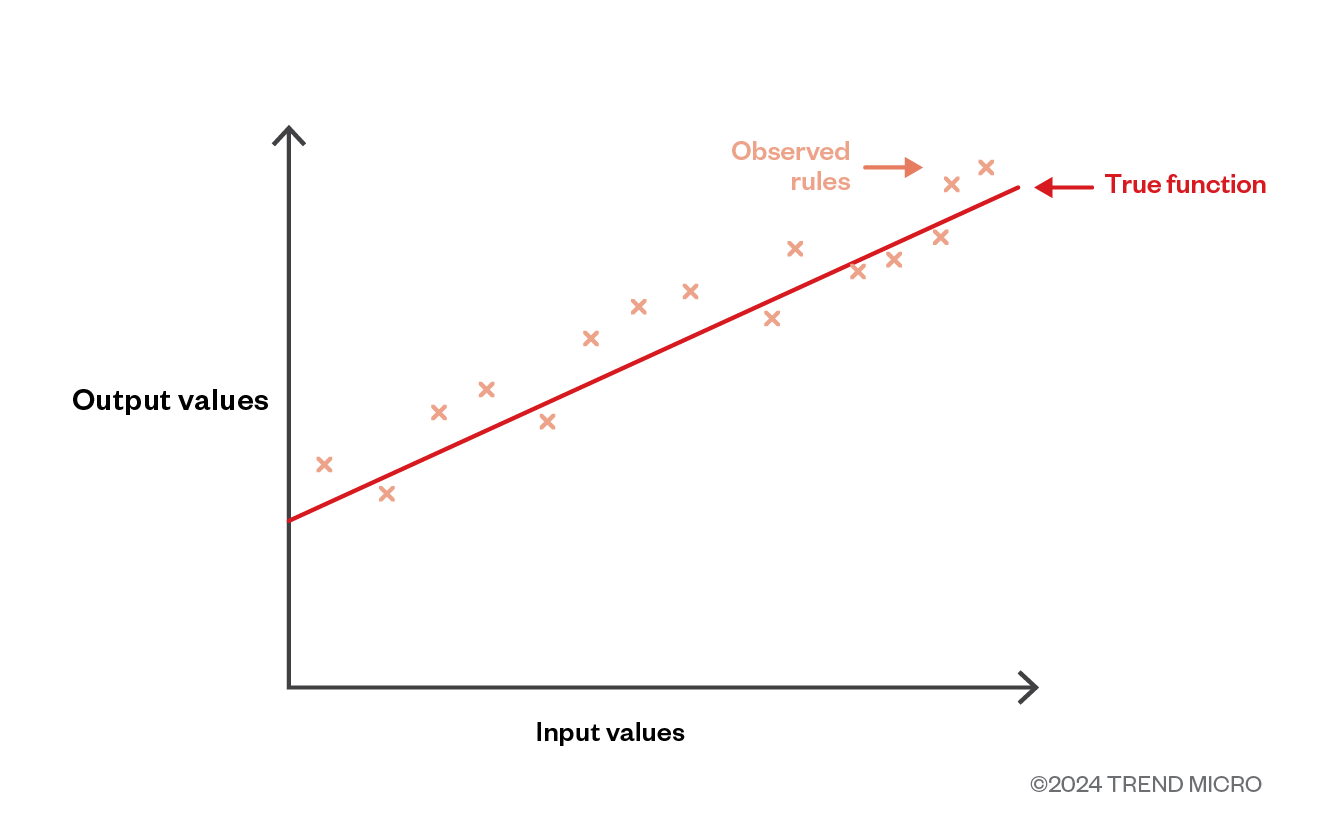
Figure 1. In learning with errors, an input value is littered with noise to create an output value.
We can visualize this as a function that takes input values and outputs the result. The true function, represented by the red line, is secret, and we add noise, represented in orange, to create the output value. For more complicated equations, the error makes it difficult to recover the true function accurately.
The lattice problem
This scheme hides information within a mathematical grid, a lattice, that makes it extremely difficult to unlock without the right key. Figure 2 shows a two-dimensional lattice, where vectors b1 and b2 are the basis vectors. The lattice problem requires looking for the shortest vector to get to the vector of origin by combining the two basis vectors. While doable but already difficult in a two-dimensional space, the problem becomes increasingly complex in higher dimensions. This problem is known to be NP-Hard, a term that refers to a class of problems where no known algorithm is efficient enough to solve it in practical time, but if a solution is provided (in the case of our discussion, a basis vector that will act as a key), the problem can be verified in polynomial time.
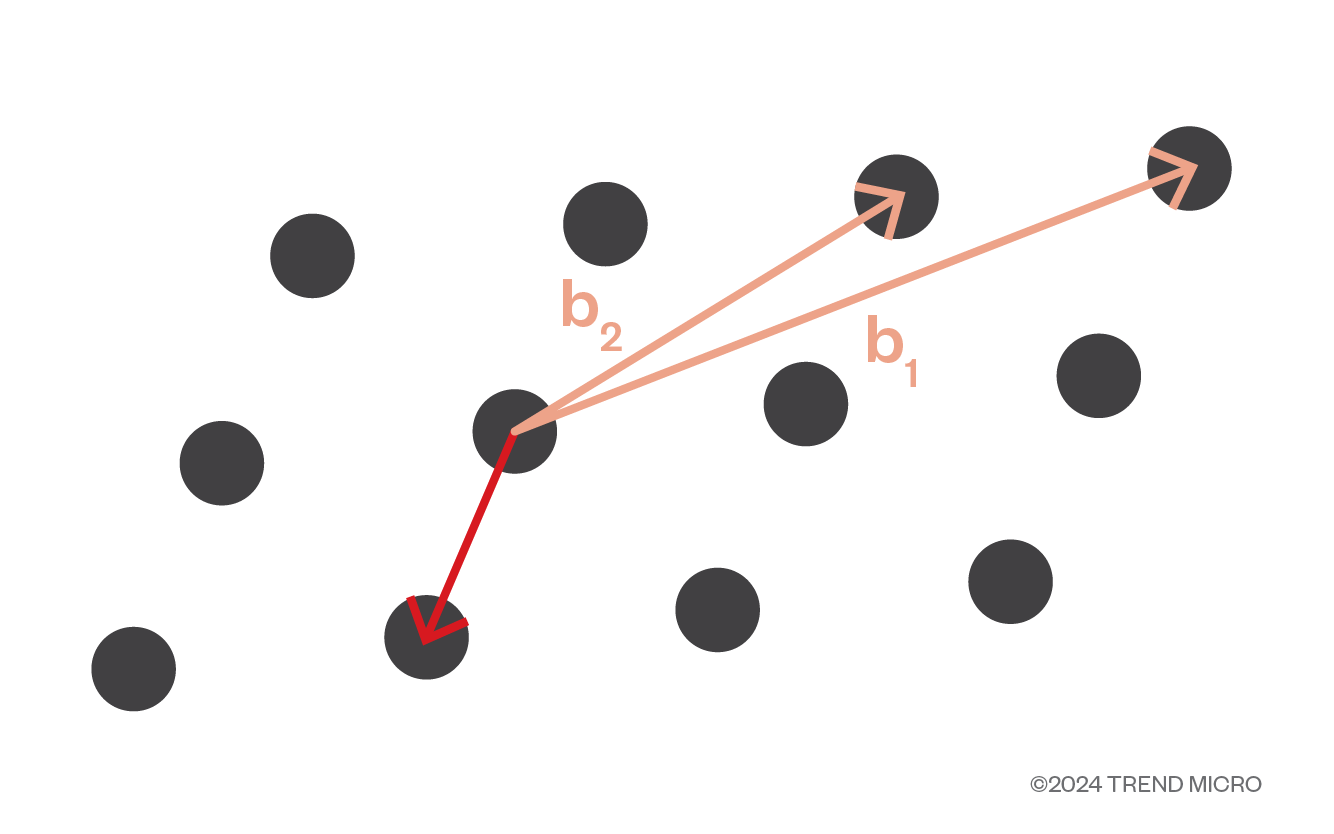
Figure 2. The lattice problem requires looking for the shortest vector by combining the two basis vectors to get to the vector of origin.
Hash-based
Hash-based cryptography is the generic term for constructions of cryptographic primitives based on the security of hash functions. All the currently used cryptographic hashes are considered quantum resistant if sufficiently large keys are used. Doubling the key size is usually enough, but the larger the key, the more unique a hash value can be to the input data, and the smallest of changes will produce a significantly different hash value. So, we can use hash-based cryptography to construct digital signature schemes such as the Merkle signature scheme, zero-knowledge proofs (ZKP), and computational integrity proofs (CIP). The seminal works by Merkle and Lamport that were developed in the 1970s already explored this, but the idea and concept was “rediscovered” and further refined with the search for post-quantum cryptography.
Code-based
The code-based approach to cryptography is derived from correcting transmission errors when communicating over a noisy channel. Instead of an unintentionally noisy channel, we intentionally introduce random noise into the stream of cyphertext containing hidden error correcting codes. Without knowing the error correction scheme, it is very difficult to decode the message, and this is referred to the decoding problem. While code-based approaches have been around since at least 1978 with Robert McEliece’s research, this problem is also known to be NP-Hard. There is also no known quantum solution to solve this problem in practical time.
Isogeny-based cryptography
Elliptic-curve cryptography (ECC) is a type of encryption that uses the points in an elliptic curve to scramble a message and secure data. ECC itself is also broken by quantum computing, by way of connecting two different but related elliptic curves, or isogenous curves.
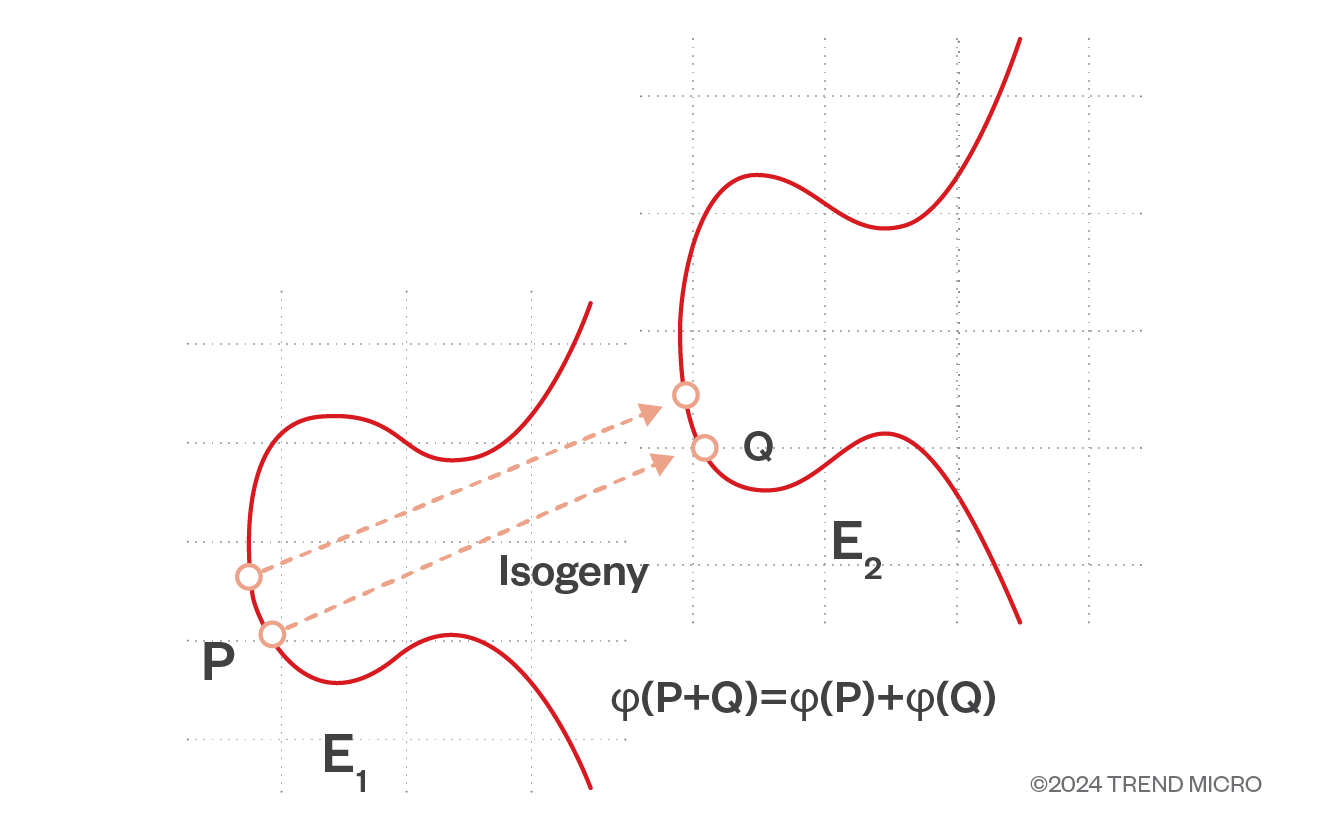
Figure 3. Isogeny-based cryptography requires looking for the rational map between two elliptic curves that maintains their mathematic properties to allow for both curves to communicate and share information securely.
Isogeny-based encryption is a variant of ECC that uses this concept; it relies on it being easy to come up with a set of isogenies and elliptic curves, but very hard to find the isogenies given only the elliptic curves. Secret keys are derived from a randomly chosen isogeny and the public key is derived from the target of these isogenies. The keys used in this encryption are about the same size as those used in current cryptography, which makes it an attractive option for securing data. Finding the isogenies used to compute points on two known target curves is akin to computing the discrete logs of values in a Diffie-Hellman (DH) key exchange protocol. There is no relation between the problem of finding the isogenies and problems with known good quantum computing solutions and are therefore considered quantum resistant. It’s important to note that this description of isogeny-based encryption is simplified for brevity; further explanation will require a deeper and lengthier diver into elliptic curve cryptography.
Comparing Post-Quantum Cryptography Candidates
Quantum computers with a large enough capacity to break our current cryptography do not exist yet, so why should we care?
There is a scenario where an attacker can capture all the internet traffic from a connection, including the key-establishment and the symmetrically encrypted data stream, and when quantum computers of sufficient size exist in the future, the attacker will be able to find the shared key within the captured internet traffic and decrypt the data stream with it. We call this attack on forward-secrecy a “harvest” attack. As such, there is therefore a need for quantum resistant key establishment and digital signing schemes
The National Institute of Standards and Technology (NIST) initiated a selection process for post-quantum cryptography in 2017 with nearly 70 candidates that have been narrowed down to 15 candidates after the third round of evaluations was completed in 2022. Eight of the 15 candidates are still under evaluation, while seven candidates are already slated for standardization.
Equally important, in 2021 the Internet Engineering Task Force (IETF) discussed a hybrid approach to post-quantum cryptography in TLS 1.2, a prudent method to mitigate any unknown weaknesses in any single algorithm. This idea has been echoed by the German BSI (Federal Office for Information Security) and French ANSSI (Cybersecurity Agency).
KEM algorithms
Key exchange cryptography is also known as key establishment methodology or key encapsulation mechanism (KEM), where a key is agreed on that can be used for symmetric encryption between two parties. It is a subset of what public key cryptography can do and we currently use algorithms like Diffie-Hellman or RSA (Rivest–Shamir–Adleman) for this.
The current selection of KEM finalists in the NIST post-quantum cryptography (PQC) standardization are CRYSTALS-Kyber, NTRU, and Saber (lattice-types), and Classic McEliece (code-based). However, only CRYSTALS-Kyber was selected for standardization in the third round.
CRYSTALS-Kyber is now considered a primary algorithm and has been given the Federal Information Processing Standards (FIPS) number 203. This lattice-based scheme has a LWE module for key generation. Its origins date back to 2005 but the NIST submission was based on a paper released in 2018, making it a young algorithm by cryptography standards. The performance is relatively good, but like the other structured lattice KEMs, Kyber’s public key is in the order of a thousand bytes — still small compared to other candidates, with bandwidth requirements also on the lower side. Kyber has comparatively fast key generation, encapsulation and decapsulation in software implementations and there are already some optimizations for various software and hardware solutions. It can be implemented on field-programmable gate arrays (FPGA) effectively. Kyber’s authors put effort into showcasing its security, so it is considered mature despite the relatively new approach. Earlier this year, however, Yilei Chen published algorithms for finding solutions to the lattice problem on a quantum computer. While this is a step in the direction of breaking lattice-based schemes such as Kyber, the inventors have built in various safeguards. For example, Kyber combined LWE with the lattice-based scheme to keep it safe by our current state of knowledge; but it should be noted that combining schemes is still a new field of cryptography.
Classic McEliece was proposed in 2017 but based on the original McEliece algorithm from 1978. This makes it different from many of the other proposals that are LWE and lattice-based. It remains to be seen if it eventually becomes a standard. Classic McEliece, along with other code-based BIKE and HQC, have advanced to the fourth round for further consideration.
Isogeny-based SIKE also initially advanced to the next round as an alternate candidate, but was then retracted when an attack against it was found. There are currently no further isogeny-based schemes in the race, but research continues.
Lattice-type FrodoKEM and NTRU Prime were designated alternatives but will not be standardized. Even though FrodoKEM is now out of the NIST-PQC race, the German BSI and the French ANSSI still consider it a good candidate. There have been appeals to reinstate its consideration in NIST’s fourth round.
SIG algorithms
Meanwhile, the digital signature schemes are referred to as SIG in the NIST standardization process, where CRYSTALS–Dilithium, FALCON, and SPHINCS+ have been selected for standardization.
CRYSTALS-Dilithium is a lattice-based scheme based on the Fiat-Shamir paradigm to keep key sizes manageable. It uses short keys and signatures like FALCON but does not require floating point operations. This makes it easier to implement on various CPUs and makes it efficient; NIST strongly recommends Dilithium for implementors. Dilithium is being standardized as FIPS 204.
FALCON is also a lattice-based scheme but is based on the "hash and sign" paradigm. It requires floating point operations and has a complex internal data structure, making it difficult to implement on a variety of CPUs. However, FALCON requires the smallest bandwidth of the candidate schemes and is faster when verifying a signature, but it’s slower than Dilithium when signing. It was chosen as an alternative when lower bandwidth and higher security is required, but NIST has yet to assign it a FIPS number.
SPHINCS+ is based on the combination of various hash-based schemes that can perform key generation and validation quickly, creating short public keys, but it can be slow when signing, creating long signatures. SPHINCS+ could be tricky to implement and perform cryptanalysis on. Two attacks with specific parameters on SPHINCS+ were discovered in the third round of evaluation, making it a surprising choice for standardization, with the FIPS number 205. We assume they did this to have an alternative to the other two lattice schemes. In this case, it should be noted that care should be taken to avoid insecure parameter sets when using the algorithms.
The Internet Engineering Task Force (IETF) has proposed their own SIG algorithms: XMSS (RFC 8391) and LMS (RFC 8708). LMS is within the IETF standards, while XMSS is created for information only. These will likely remain niche algorithms, at best, in favour of the NIST and FIPS standards.
Quantum Key Exchange
An alternative to KEM is Quantum Key Exchange (QKE), which is a secure key exchange algorithm that uses the entanglement of particles to establish a shared secret that, if snooped on, will be invalidated. The invalidation happens because the attacker needs to measure the quantum state of the entangled particles, which will result in the collapse of its superposition. This algorithm is called BB84, after the authors Charles Bennett and Gilles Brassard who developed it in 1984.
QKE requires special hardware and a dedicated transmission medium, usually fiber optic cables, but a satellite link has also been successfully tested. Having been tested since the 2000s, the distance that keys can be transmitted has improved from tens of kilometers to around a thousand kilometers.
The technology has already been used in practice: in 2023, Toshiba, the BT Group (formerly British Telecom) and HSBC bank (Hongkong and Shanghai Banking Corporation Limited) tested a secure link in London where symmetric keys were exchanged using QKE, and the data is encrypted over any standard communication link using a symmetric cipher.
In the foreseeable future, this will not be the technology that secures our everyday web server connections but can secure connections between large hubs of computing such as data centers, and it could also connect a data center to an office complex. The current requirement for specialized equipment and a dedicated fiber optic cable makes personal use impossible for the moment. This technology is related to the quantum internet, but to avoid confusion, we refer to it as Quantum Key Distribution Network.
Groundwork laid for a post-quantum cryptographic future
The Open Quantum Safe (OQS) project has taken all finalists and a few alternate candidates and added them to liboqs, an open-source C library for quantum-safe cryptographic algorithms implemented with various parameters for various CPUs. Support for a variety of CPUs beyond the x86 architecture is improving but many smaller IoT processors still have limited support, mostly because of memory limitations.
Open Quantum Safe has also forked the Open Secure Sockets Layer (OpenSSL) and Secure Shell (SSH) projects and added their respective libraries. This will be useful for testing both compatibility as well as performance, but liboqs is not yet recommended for production use.
Various commercial vendors of cryptography have started implementing PQC. These can be tracked at the Public Key Infrastructure (PKI) Consortium’s website. Both Cloudflare and Amazon Web Services (AWS) claim to have implemented the finalists’ algorithms. The communications app, Signal, has started using CRYSTALS-Kyber for their message security. Likewise, Apple has also started using Kyber in their iMessage communications app; but they opted to call it PQ3.
Upgrading to PQC
In the last decade, we have gone from encrypted connections being optional to being nearly ubiquitous. Ten years ago, changing a cryptographic algorithm would have been comparatively simple compared to how it is today. Now, browsers use Transport Layer Security (TLS) with either an HTTPS or QUIC connection whenever possible, cloud data is encrypted at rest and in transport, and digital signing of software is the norm. Changing our cryptography now will be a huge task.
The threat landscape now also contains many state actors who may be able and willing to “harvest” network traffic to decrypt it later when quantum computers become available. This determines whether you decide to require forward-secrecy, such as requiring that encrypted messages stay unreadable for unauthorized viewers for at least five years.
The good news is that many individuals and companies may not have to do anything. Today, some products are starting to integrate PQC algorithms. Google recently integrated CRYSTALS-Kyber into version 116 of Chromium, which means that Google Chrome and other browsers based on Chromium will have PQC support. On the server side, some cloud providers like Google, Amazon and Cloudflare have enabled the same algorithm on the server so that this traffic will be forward-secret in the future.
For instance, Figure 3 shows what Cloudflare’s test page for PQC negotiation looked like before the upgrade of Chrome, while Figure 4 shows what it looks like after the upgrade and manually activating the Kyber (called X25519Kyber768Draft00) algorithm.

Figure 4. Cloudflare’s test page for PQC negotiation before Chrome’s upgrade

Figure 5. Cloudflare’s test page for PQC negotiation after the upgrade and manually activating the Kyber algorithm
Vendors will be doing many of the migrations to PQC for us using nascent libraries or their own implementations; however, enterprises should understand their exposure and threat model to make sure that some legacy applications do not prevent the upgrade. A mature organization should have a plan for upgrading their cryptography, regardless of the reasons.
Does your organization need to upgrade to PQC?
Ultimately, this is a business strategy decision, and it depends on a company’s threat model. If forward-secrecy is vital to the organization, early adoption will be vital. If not, enterprises can opt to wait for vendors to implement PQC and roll it out within their systems gradually. An informed decision involving business leadership will ensure its success.
Preparing for the upgrade
The first stage in upgrading to new algorithms is to identify cryptographic algorithm use. For the purposes of upgrading to post-quantum cryptography, we must first look at existing public key cryptography. We need to know what self-managed cryptography is used, by whom, where, and for what assets. We must also identify the respective value of the assets being encrypted.
Finding interoperations
Next, we need to know how systems are communicating with each other: If a server supports PQC but a client does not, an enterprise cannot enforce PQC. While the largest cloud providers are being proactive, some services may not get updated, which needs to be determined.
Identifying performance issues
We know that all PQC algorithms have larger key sizes and requires more CPU and memory capacity to compute compared to current algorithms. The performance impact is of concern on servers that need to establish numerous connections. The server hardware will have to be scaled up, or cryptographic co-processors may be needed if these exist for PQC by then. Some cloud providers offload the TLS connection to specialized servers, which could also alleviate the problem.
Risk analysis
Enterprises need to understand the risk to their respective businesses. Some questions to consider are:
- Do certain applications have forward-secrecy requirements beyond the expected emergence of quantum computers?
- Do any documents or code need re-signing, and can the systems understand PQC signatures?
These evaluations should be collected in a report and used as a reference to help identify further priority actions.
Continuous testing
Before execution, the upgrade plan needs to be tested to identify and negotiate which algorithm will be used by each library, as well as enabling and monitoring the logs to make sure a PQC algorithm is used when it is expected. Stress testing connections to see if the larger keys and lower performance has negative impacts is another important test.
Plan ahead
NIST will most likely standardize the PQC algorithms in 2024 or 2025. The German BSI, French ANSSI and Japanese CRYPTREC are likely to adopt the same guidelines. Until that happens, we don’t expect any of the PQC algorithms to be integrated into mainstream cryptographic libraries, but a good time to start planning for post-quantum cryptography is still now.
Concluding the series
We cannot say for certain when large enough quantum computers will exist, or even if that goal is attainable within the next few generations. By our estimate, it looks likely that we’ll see smaller, still useful machines, in a few years. Larger, more universal machines may follow in a decade. While that sounds like a long way away, changing cryptography in an enterprise is no small feat and should be tackled as early as possible. Furthermore, the benefits are already tangible if we better understand our cryptographic stance, especially considering that so much of security rides on good cryptography.
Like it? Add this infographic to your site:
1. Click on the box below. 2. Press Ctrl+A to select all. 3. Press Ctrl+C to copy. 4. Paste the code into your page (Ctrl+V).
Image will appear the same size as you see above.
 Cellular IoT Vulnerabilities: Another Door to Cellular Networks
Cellular IoT Vulnerabilities: Another Door to Cellular Networks AI in the Crosshairs: Understanding and Detecting Attacks on AWS AI Services with Trend Vision One™
AI in the Crosshairs: Understanding and Detecting Attacks on AWS AI Services with Trend Vision One™ Trend 2025 Cyber Risk Report
Trend 2025 Cyber Risk Report CES 2025: A Comprehensive Look at AI Digital Assistants and Their Security Risks
CES 2025: A Comprehensive Look at AI Digital Assistants and Their Security Risks